相似矩阵

Author: abklis

相似矩阵

特征值与特征向量

设 $A$ 为 $n$ 阶方阵,如果存在数 $\lambda$ 以及非$0$ 列向量 $\xi$ 使得 $A \xi = \lambda \xi$ ,则称 $\lambda$ 为 $A$ 的一个特征值, $\xi$ 是 $A$ 的属于特征值 $\lambda$ 的一个特征向量

注： $n$ 阶矩阵的特征值 $\lambda$ 有且仅有 $n$ 个，但 $\xi$ 有无数个，且每一个 $\lambda$ 都拥有无数个属于它的特征向量 $\xi$ .

求特征值特征向量方法先求出所有的特征值 $\lambda$ ，再计算每个特征值对应的 $\xi$

$$A \xi = \lambda \xi \Leftrightarrow (A - \lambda E )\xi = 0 \stackrel{\xi \neq 0}{\Longrightarrow}A - \lambda E = 0$$

然后解出特征值 $\lambda$ ,再把 $\lambda$ 代回方程 $(A - \lambda E )\xi = 0$ ,从而解得 $\xi$
一些重要结论:

特征值之和等于 $A$ 的对角线元素之和，特征值之积等于行列式 $|A|$
属于不同特征值的特征向量，一定线性无关；
属于同一个特征值的特征向量，组合起来以后仍然是该特征值的特征向量
属于不同特征值的特征向量，组合起来以后不再是矩阵A的特征向量
若 $\lambda$ 是 $A$ 的 $k$ 重特征值，则 $\lambda$ 最多只有 $k$ 个线性无关的特征向量
$A$ 与 $A^T$ 有相同特征值，$AB$ 与 $BA$ 有相同特征值

$A$	$aA+bE$	$A^k$	$f(A)$	$A^{-1}$	$A^{*}$	$P^{-1}AP$
$\lambda$	$a \lambda +b$	$\lambda ^k$	$f(\lambda)$	$\lambda ^{-1}$	$\frac{\|A\|}{\lambda}$	$\lambda $
$\xi$	$\xi$	$\xi$	$\xi$	$\xi$	$\xi$	$P^{-1}\xi$

相似对角化

矩阵的相似:对于 $n$ 阶方阵 $A,B$ ,若存在可逆矩阵 $P$ ,使得 $P^{-1}AP=B$ ,则称 $A$ 与 $B$ 相似,记作$A \sim B$
相似对角化:对于 $n$ 阶方阵 $A$ ,若存在可逆矩阵 $P$ ,使得 $P^{-1}AP= \Lambda$ ($\Lambda$ 为对角矩阵),则称 $A$ 可相似对角化,记作 $A \sim \Lambda$

如何判断矩阵能否相似对角化?

$$ A\text{可相似对角化} \Leftrightarrow P^{-1}AP= \Lambda \color{red}{\Longrightarrow} \color{black}AP=P\Lambda \\ \stackrel{\text{对P按列分块}}{\Longleftrightarrow} A \begin{pmatrix} \xi_1,\xi_2,\cdots,\xi_n \end{pmatrix} = \begin{pmatrix} \xi_1,\xi_2,\cdots,\xi_n \end{pmatrix} \begin{pmatrix} \lambda_1\quad\quad\quad\quad\quad\\ \quad \lambda_2 \quad \quad\\ \quad\quad\quad\ddots\quad\\ \quad\quad\quad\quad\quad\quad \lambda_n \end{pmatrix} $$

从而得出

$$ \begin{pmatrix} A\xi_1,A\xi_2,\cdots,A\xi_n \end{pmatrix} = \begin{pmatrix} \lambda\xi_1,\lambda\xi_2,\cdots,\lambda\xi_n \end{pmatrix}\\ \text{即} A\xi_i=\lambda\xi_i(i=1,2,\cdots,n) $$

不难发现,最后这个形式恰好和特征值特征向量定义相吻合,要证明矩阵能相似对角化,只需要让上述推导过程中的 $\color{red}{\Longrightarrow}$ 变成 $\Leftrightarrow$ ,也就是让 $P$ 可逆即可.

如何保证 $P$ 可逆呢,只要让 $\xi_i(i=1,2,\cdots,n)$ 线性无关即可,又由于两个高亮结论,可得只需要保证k重特征值有k个线性无关的特征向量即可.

一些重要性质和结论:

若 $A$ 有 $n$ 个无关的特征向量,则 $A$ 一定可以相似对角化(充要条件)
实对称矩阵一定可以相似对角化(充分条件)
若 $A \sim B$ ,则 $r(A)=r(B),|A|=|B|,tr(A)=tr(B)$ (主对角线元素之和),$A$ 和 $B$ 的特征值相同,$A^* \sim B^*,A^{-1}\sim B^{-1} ,A^T \sim B^T$

实对称矩阵的相似对角化

实对称矩阵:元素全部为实数的对称矩阵

正交阵: $Q^TQ=QQ^T=E$ ,也就是 $Q^T=Q^{-1}$

实对称矩阵的一些性质:

特征值全为实数
取自不同特征值的特征向量全部正交
一定可以正交
对于实对称矩阵 $A$ ,一定存在正交矩阵 $Q$ ,使得

$$ Q^TAQ = \Lambda= \begin{pmatrix} \lambda_1\quad\quad\quad\quad\quad\\ \quad \lambda_2 \quad \quad\\ \quad\quad\quad\ddots\quad\\ \quad\quad\quad\quad\quad\quad \lambda_n \end{pmatrix}\\ $$

其中正交矩阵 $Q$ 中的特征向量 $(\overrightarrow{e_1},\overrightarrow{e_2},\cdots,\overrightarrow{e_n})$ 均为单位向量,并且全部正交

那么如何得到正交矩阵 $Q$ 呢? 不难发现,我们只需要把 $P$ 中的 $\xi_i(i=1,2,\cdots,n)$ 全部变成正交的单位向量即可,变成单位向量简单,让 $\dfrac{\overrightarrow{\xi_i}}{|\overrightarrow{\xi_i}|}$ 就可以了,麻烦的就是让它们正交化,下面就简单介绍一下二维向量的施密特正交化(高纬度的我也想象不出来)

施密特正交化

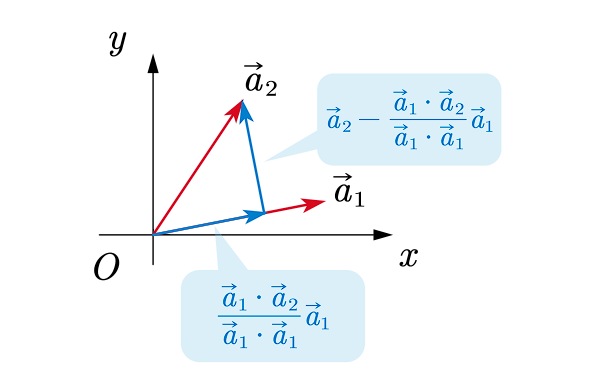
$\alpha_1 \cdot \alpha_2$ 再除以 $|\alpha_1|$ 再乘以 $\dfrac{\overrightarrow{\alpha_1}}{|\overrightarrow{\alpha_1}|}$ ,便可得到 $\dfrac{\alpha_1 \cdot \alpha_2}{\alpha_1^2}\alpha_1$

$\beta_2$ 只需要用 $\alpha_2- \dfrac{\alpha_1 \cdot \alpha_2}{\alpha_1^2}\alpha_1$ 即可得到

综上:$\beta_1=\alpha_1,\beta_2=\alpha_2-\dfrac{\alpha_1 \cdot \alpha_2}{\alpha_1^2}\alpha_1=\alpha_2-\dfrac{ \beta_1\cdot \alpha_2}{\beta_1^2}\beta_1$

对于 $n$ 维的向量施密特正交化:

$$ \beta_1=\alpha_1\\ \beta_2=\alpha_2-\dfrac{ \beta_1\cdot \alpha_2}{\beta_1^2}\beta_1\\ \cdots\cdots\\ \beta_n=\alpha_n-\dfrac{\beta_1 \cdot \alpha_n}{\beta_1^2}\beta_1-\dfrac{\beta_2 \cdot \alpha_n}{\beta_2^2}\beta_2-\cdots-\dfrac{\beta_{n-1} \cdot \alpha_n}{\beta_{n-1}^2}\beta_{n-1} $$

二次型

二次型的定义:

含有 $n$ 个变量的二次齐次多项式,例如: $a_1x_1^2+a_2x_1x_2+a_3x_2^2$ 这种

二次型矩阵

定义:一个定义在 $R^n$ 上的二次型,如果它在向量 $x$ 处的值可由表达式 $Q(x)=x^TAx$ 计算,其中 $A$ 为 $n \times n$ 的对称矩阵,那么对称矩阵 $A$ 就称为该二次型对应的矩阵

不妨举两个例子加深对二次型矩阵的理解:

eg1:

$$ x= \begin{bmatrix} x_1\\x_2 \end{bmatrix} ,A= \begin{bmatrix} 3&-2\\-2& 7 \end{bmatrix} $$

求x^TAx

$$ x^TAx= \begin{bmatrix} x_1&x_2 \end{bmatrix} \begin{bmatrix} 3&-2\\-2& 7 \end{bmatrix} \begin{bmatrix} x_1\\x_2 \end{bmatrix}= 3x_1^2+7x_2^2-4x_1x_2 $$

eg2:

取 $Q(x)=5x_1^2+3x_2^2+2x_3^2-x_1x_2+8x_2x_3$ ,写出 $x^TAx$ 形式的二次型

不难发现,$x_i^2$ 的系数是在主对角线(即第 $i$ 行第 $i$ 列)上的

为了让 $A$ 对称,$x_ix_j(i\neq j)$ 的系数必须平均分配给矩阵 $A$ 的第 $i$ 行第 $j$ 列和第 $j$ 行第 $i$ 列

易得

$$ Q(x)=x^TAx= \begin{bmatrix} x_1&x_2&x_3 \end{bmatrix} \begin{bmatrix} 5&-\dfrac{1}{2}&0\\ -\dfrac{1}{2}&3&4\\ 0&4&2 \end{bmatrix} \begin{bmatrix} x_1\\x_2\\x_3 \end{bmatrix} $$

在某些情况下,没有交叉项的二次型(即二次型对应的矩阵为对角矩阵)会显得更容易运用,我们称这样的二次型为标准形,要想消去交叉项,我们可以通过一些变量代换来实现

二次型标准化的方法

变量代换通常是 $x=Py$ 或者 $y=P^{-1}x$ ,其中 $P$ 是可逆矩阵如果用变量代换处理 $x^TAx$ 就得到了 $x^TAx=(Py)^TA(Py)=y^TP^TAPy=y^T(P^TAP)y$

要得到标准形,只需要让 $P^TAP$ 这个矩阵为对角矩阵$\Lambda$ 即可

合同对角化:如果存在一个可逆矩阵 $P$ ,使得 $P^TAP=\Lambda$ ,此时称 A 可以合同对角化

正交变换法: 我们注意到,在实对称矩阵的性质中,有一条“对于实对称矩阵 $A$ ,一定存在正交矩阵$Q$,使得 $Q^TAQ = \Lambda$” 那么就可以通过变换 $x=Qy$ 将二次型变为标准形,简要总结一下步骤:

根据二次型 $f(x_1,x_2,x_3)$ (以三元二次型为例)写出实对称矩阵 $A$
求正交矩阵 $Q$ ,使得 $Q^TAQ=\Lambda$
下结论,做变换 $x=Qy$ ,二次型 $f(x_1,x_2,x_3)$ 就变成了标准形 $f(y_1,y_2,y_3)=\lambda_1 y_1^2+\lambda_2 y_2^2+\lambda_3 y_3^2$

不难发现,其中的 $\lambda$ 还恰好是矩阵 $A$ 的特征值

简单的来做个题吧!

已知二次型 $f(x_1,x_2,x_3)=x_1^2+5x_2^2+5x_3^2+2x_1x_2-4x_1x_3$ ,利用正交变换 $x=Qy$ ,将其化为标准形

(懒得打字了)

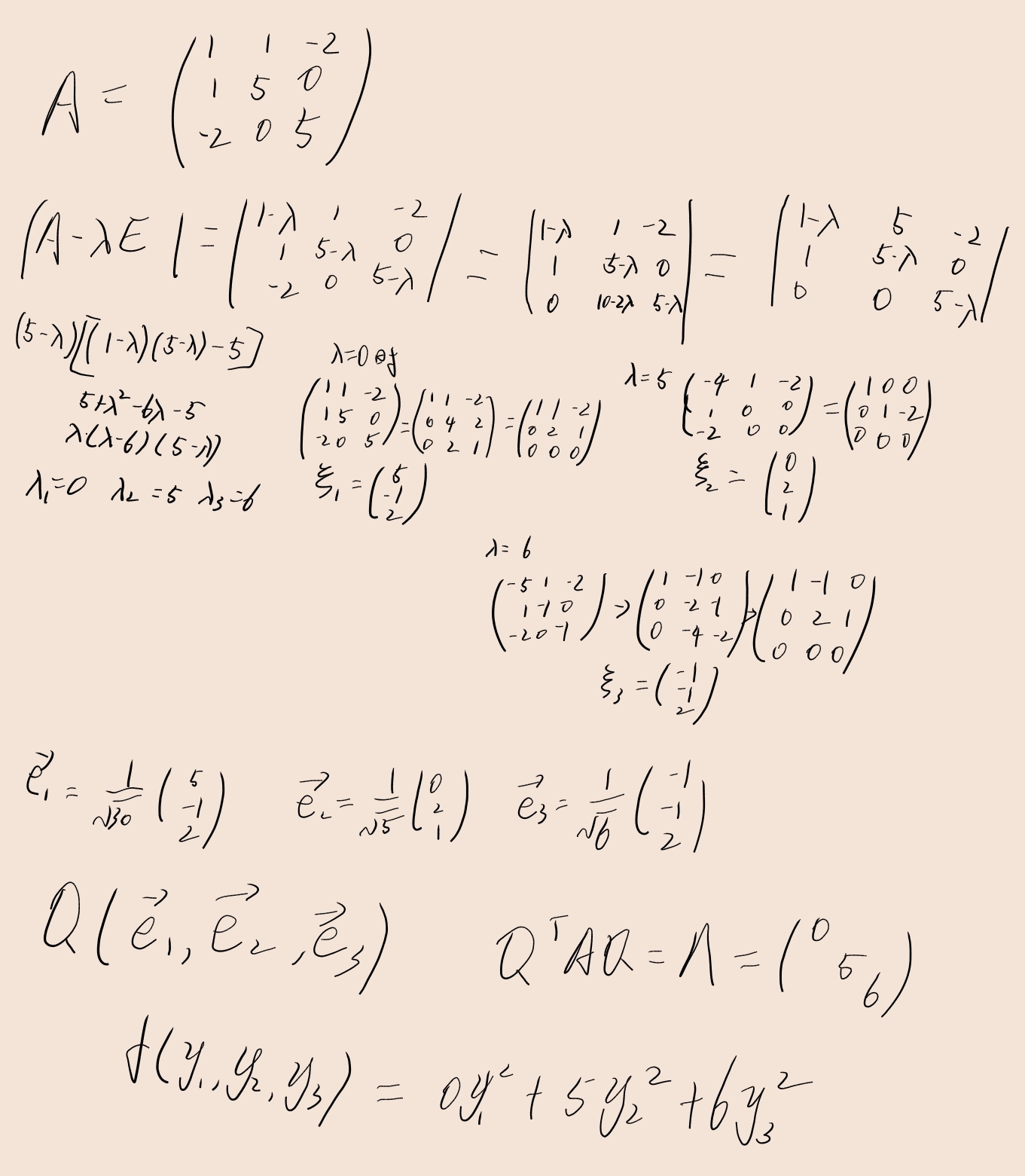
配方法:

就初高中学的配方,需要注意的就是平方项前面的系数就不一定是矩阵 $A$ 的特征值了

eg1:

已知二次型 $f(x_1,x_2,x_3)=x_1^2+5x_2^2+5x_3^2+2x_1x_2-4x_1x_3$,将其化为标准形

$$ \begin{aligned} \text{原式}&=(x_1^2+2x_1x_2-4x_1x_3)+5x_2^2+5x_3^2\\ &=[(x_1+x_2-2x_3)^2-x_2^2-4x_3^2+4x_2x_3]+5x_2^2+5x_3^2\\ &=(x_1+x_2-2x_3)^2+4x_2^2+x_3^2+4x_2x_3\\ &=(x_1+x_2-2x_3)^2+(2x_2+x_3)^2+0x_3^2 \end{aligned} $$

令

$$ \begin{cases} y_1=x_1+x_2-2x_3\\ y_2=2x_2+x_3\\ y_3=x_3 \end{cases} $$

即做变换

$$ \begin{cases} x_1=y_1-\dfrac{1}{2}y_2+\dfrac{2}{5}y_3\\ x_2=\dfrac{1}{2}y_2-\dfrac{1}{2}y_3\\ x_3=y_3 \end{cases} $$

即可化为 $f=y_1^2+y_2^2$

eg2:

用配方法化二次型 $f(x_1,x_2,x_3)=2x_1x_2+2x_1x_3-6x_2x_3$ 为标准形

此题没有平方项,我们先利用平方差公式搞出平方项再说

$$ \begin{cases} x_1=y_1+y_2\\ x_2=y_1-y_2\\ x_3=y_3\\ \end{cases} $$

得到 $f=2y_1^2-2y_2^2-4y_1y_3+8y_2y_3$

再像 eg1 那样配方得 $f=2(y_1-y_3)^2-2(y_2-2y_3)^2+6y_3^2$

令

$$ \begin{cases} z_1=y_1-y_3\\ z_2=y_2-2y_3\\ z_3=y_3\\ \end{cases} $$

即

$$ \begin{cases} x_1=z_1+z_2+3z_3\\ x_2=z_1-z_2-z_3\\ x_3=y_3\\ \end{cases} $$

得标准型 $f=2z_1^2-2z_2^2+6z_3^2$

惯性定理和规范形

惯性定理:二次形的标准形不唯一,但标准形的正负项的个数是唯一确定的,分别称之为二次形的正,负惯性指标
规范形:正系数全是 $1$ 且负系数全是 $-1$ 的标准形，称为规范形.

虽然标准形并不唯一，但规范形一定是唯一的

对于任何一个标准形,都可以经过可逆线性变换化成规范形

正定二次型和正定矩阵

定义:对于二次型 $Q(x)=x^TAx$ ,若对任意的 $x\neq 0$ ,恒有 $x^TAx > 0$ ，则称该二次型 $x^TAx$ 为正定二次型，并将该二次型对应的矩阵 $A$ 称为正定矩阵
如何判断二次型是否正定?

对任意的 $x\neq 0$ ,恒有 $x^TAx \neq 0$
$A$ 的特征值 $\lambda$ 全为正
$n$ 阶矩阵 $A$ 的正惯性指标 $p=n$
$A$ 的顺序主子式均大于零